Giusseppe
Una carta de mujer de Marceline Desbordes-Valmore

Te escribo, aunque ya sé que ninguna mujer
debe escribir;
lo hago, para que lejos en mi alma puedas leer
cómo al partir.No he de trazar un signo que en ti mejor grabado
no exista ya.
De quien se ama, el vocablo cien veces pronunciado
nuevo será.La dicha sea contigo; yo sólo he de esperar,
y aunque distante,
yo me siento ir a ti para ver y escuchar
tu paso errante.¡Jamás la golondrina al cruzar el sendero
pueda apartarte!
Será mi fiel cariño que pasará ligero
para rozarte…Tú te vas, como todo se va… Su éxodo emprenden
la luz, la flor;
el estío te sigue; las tormentas sorprenden
mi triste amor.De esperanza y zozobra suspira mientras tanto
el que no ve…
Repartámoslo bien: a mí me queda el llanto,
a ti la fe.Yo no quiero que sufras, que está muy arraigado
mi amor por ti.
Quien desea dolores para el ser adorado
guarda odio a sí.
Nota: Traducción de Mauricio Bacarisse (1921)
Hoy acabo de encontrarme con esta poeta en el ensayo, que en su día (es decir, hace tiempo) leí titulado «Los Poetas Malditos» de Paul Verlaine. No recordaba que en el mismo hubiese una mujer. Por supuesto, no tengo ningún libro de esta mujer, de quien apenas hay ediciones. Este poema no me gusta mucho, pero tampoco me encantan los poemas de Verlaine quien aparece bajo el pseudónimo de «Pobre Lelian».
En los poetas malditos no estaban (como yo creía erróneamente recordar) ni Baudelaire, ni Lautreamont.
Algo avergonzado de mi desmemoria… (¿será parte del sesgo que más temo?)
Romance inapropiado
Las orejas y el móvil
tienen un romance inapropiado:
se tocan cuando no deben
hacen lo que no corresponde
suspiran en su oído
palabras secretas
laten con calor acompasado
se humedecen
con lascivia de colegiales
sudan al rozarse
sin denuedo
y enmudecen
acompasadamente
después de abandonar
el campo de batalla.
Probabilidades
Siempre se me han dado mal los problemas de probabilidad, quizá (casi seguro) porque no los estudié durante el periodo de formación que más aproveché de mi vida: la adolescencia. Así que cuando me preguntan algo de este tipo me echo a temblar (con toda probabilidad). Cada año me toca volver a hojear apuntes al respecto para poder impartir las clases particulares de matemáticas que, cada vez más, incluyen más contenido de probabilidad y estadística, incluso en las matemáticas «de ciencias».
Pero lo que no me podía esperar era que un alumno de los talleres de poesía me preguntase (por si yo lo sabía) cuál era la probabilidad de que, tirando 5 tetraedros numerados del 1 al 4, saliese al menos un uno.
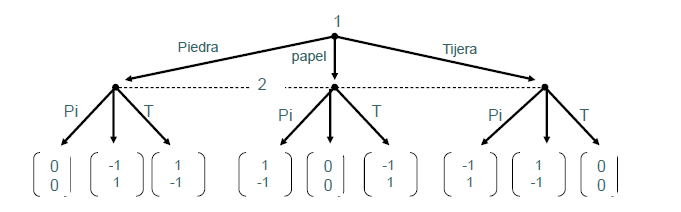
Como estaba centrado en el taller de escritura, no quise dedicarle mucho tiempo y tan sólo le dije que se podía resolver mediante diagrama de árbol (con 5 tiradas sucesivas) donde cada rama tendría un peso probabilístico del 25%. Posteriormente, le dije que podía simplificarse como un problema binario (uno 25% / no-uno 75%).
Con eso, sin mucho más, él me dijo que había realizado una simulación, donde, tras 100 millones de iteraciones, obtenía 0.76268608, es decir, aproximadamente, 76,27% de probabilidad de obtener, al menos, un uno.
No obstante, me quedé pensando que era un problema mucho más sencillo de lo que yo había estimado, si se consideraba que la probabilidad de que salga al menos un uno es equivalente al total (100%) menos la probabilidad de que no te salga un uno, es decir:
P(UNO) = P(TOTAL) – (P(NO-UNO))NumEventos = 1 – (0,75)5 = 0,7626953125 ≅ 76,27%
pero que difiere de su simulación en una diezmilésima.
Lo que más me ha interesado de esta pregunta es que resuelve muchas de mis dudas (no cuantitativamente) sobre la probabilidad de tener un accidente a lo largo de la vida o cortarse cocinando, o caerse en una caminata…
Y es que si pudiésemos cuantificar, por ejemplo, en un 99,999% la probabilidad de no caerse en un paso durante una caminata, obtendríamos que, en una ruta de unos 10.000 pasos, sería del:
P(CAERSE) = P(TOTAL) – (P(NO-CAERSE))10.000 = 1 – 0,9999910000 = 0,095163034 ≅ 9,52%
Lo que justifica, por fin, cierto miedo que le tengo a la vida, así, en general, pues es aquello que va haciendo crecer el número de eventos y, por tanto, reduciendo la probabilidad de no sufrir nunca.
De hecho, sin entrar en detalles, esta es la razón que explica el riesgo de contraer cánceres (mutaciones probables cancerígenas) y hace que no tenga demasiado en cuenta otros factores que aumentan la probabilidad de contraerlo.
La Aisa

Leo esto sobre metaversos y otras realidades virtuales desde Daimiel, Ciudad Real, donde nos ha traído un autobús de la compañía Aisa que ni tiene la tecnología ni el conocimiento necesario para estionar los billetes, no ya electrónicos sino en papel, adquiridos por Internet; ni conocer automáticamente el total de billetes emitidos, con lo que genera un overbooking de más de 30 personas que quedan en un limbo estacionario reclamando a voz en grito, cual verdulería incendiaria, sin intención de, tan siquiera, enviar un email… Y algo me dice que hay lugares donde eso del metaverso va a llegar con algo de retardo.
Y mientras, sigo insistiendo en hacer reclamaciones por el cauce apropiado, pero veo que nadie hace nada una vez que consigue que su sitio esté asegurado.
https://www.aisa-grupo.com/es/faqs/pregunta-2/-%09-como-puedo-poner-una-reclamacion-
Triste egoísmo que nos aísla y nos desprotege de abusos como este.
Yo, por mi parte, he hayado el tope de indignación que soporto y, después de varias incidencias parecidas, he decidido unánimemente no volver a ir montado en los asientos de esa infame compañía, salvo absoluta emergencia familiar e imposibilidad alternativa (pero no será por una cuestión de dinero).
ODA A IDA

Camiseta intervenida para descubrir un poema sobre cómo funciona Madrid este año.
Triste, pero cierto.
Realizado durante la acción poética titulada «Lavandelirium»
Tontunas pseudomatemáticas

El otro día encontré en una red social este presunto test matemático que, carente de contexto, no está tan bien formulado como él mismo se cree: nadie ha afirmado previamente que la operación que se realiza sea constante, que se trate de una sucesión «regular» y no de unos números colocados al azar, sin embargo, nos gusta ver patrones, sentir que el mundo está ordenado, así que nos disponemos a lanzar suposiciones (no cálculos, no vaya a ser que…) y así se propone que para el 3 corresponde el 30, el 18, etc. Pero no se ofrecen muchas razones (ninguna) para las soluciones propuestas, tan solo el resultado, como si se hubieran copiado de alguien en un examen.
Yo aventuro a suponer que lo que se hace es ir restando a cada número (partiendo de 18) un par menor, es decir, 16, 14, 12… hasta que puedo realizar el cálculo (sin álgebra mediante) para obtener una solución más o menos cutre:

Pero no me quedo muy satisfecho de no haber sido más riguroso, no haber realizado un cálculo algebraico, generalizable, pues era una sucesión (recursiva) a la que se le iba restando una progresión aritmética de distancia=-2
A lo más que he llegado es a tener algo de la forma:
Sean 18, 16, 14… los términos de la progresión aritmética donde b1=18, d=-2
tenemos que bn = b1 + d·(n-1) = 18 – 2·(n-1) = 20 – 2n
Podemos definir an = an-1 – bn, siendo a1=90.
No he logrado demostrar si esta sucesión podría tener un término general independientemente de su definición recursiva, pero tampoco le quiero dedicar mucho más tiempo. Algo me dice que seguro que sí se podría y esto me reconcomerá unas horas, pero voy a dejar que ocurra.
Paradoja
Soy una bomba de relojería a punto de explotar.
Soy un tren a punto de estrellarse.
Soy una presa a punto de desbordarse.
Soy un corazón a punto de reventar.
y sin embargo
no tengo pilas
no tengo fuerzas
no tengo energía
no tengo alma.
Lavandelirium

Lavandelirium
Génisis
En un lugar de La Mancha de nombre noble y compuesto, sentóse en torno a una mesa un grupo de Poetas a yantar y pimplar en verso. De pronto, una versificadora exclamó: «¡Diablos! ¡Me ha caído un lamparón al pantalón!» y a continuación quiso explicar a sus co-bardas (pues eran poetas féminas en su mayoría) el aprieto que dicha mancha suponía para ella. Con los violines de fondo––¿o acaso fue un arpa?––, reveló que, debido a la coyuntural crisis de suministros, se encontraba en esos momentos sin lavadora en casa por lo que se veía obligada a hacer la colada en una lavandería a la vuelta de la esquina. Y fue entonces que sonaron las maracas…
Cita
Viernes 29 de octubre a las 18:00, punto de encuentro: c/ Doctor Fourquet 24 (el huerto urbano Esta es una plaza), de ahí iremos a una Lavandería cercana
Programa
Acto poético: “Lavando versos” haremos una colada colectiva y veremos a ver qué combinación nos devuelve la lavadora… A este fin, trae retales de tela o prendas con un verso o una palabra escrita, bordada, recortada, o sugerida. Cada un@ irá leyendo sus versos/palabras antes de meter cada prenda en la lavadora.
Entre acto: “Colada collage” mientras se van lavando los versos montaremos y desmontaremos una exposición efimerísisima de collage ahí in situ (duración: 35 minutos aprox.)
Procesión solemne: “Posible homenaje a Quevedo” una vez acabada la colada, iremos en procesión, cada un@ con su cesta de ropa desde la Lavandería hasta la Plaza para tender la ropa. Posiblemente aprovechemos para hacer un homenaje a Quevedo, pero no lo prometemos (duración: 3-4 minutos)
Recital: “Tendiendo versos” una vez en la Plaza, procederemos a tender los versos de la colada, recitando sus resultados, y aprovecharemos para recitar algún que otro poema compuesto de antemano, al ser posible con temática afín al evento (duración: ¿15 minutos?)
Taller: “Collaging, que es gerundio” se ofrecerá a los asistentes un taller de collage (duración: ¿30 minutos?) (Fue suspendido el taller por condiciones climáticas adversas)
Clausura: “Volviendo a La Mancha” nos iremos a tomar cañas a un bar cercano de ese nombre (duración: ?)